Question

For a pipe system with a pump (pumping uphill), the change in elevation is 400 feet and the total head loss is 408.5 feet. Assuming gage pressure at the entrance and exit and no difference in velocity between the entrance and exit, determine the total energy transferred to the water. Estimate the required power input if the pump efficie

Answer 1

Step-by-step explanation:

From the given information;

There is no change or any difference in velocity in between the inlet and the outlet.

Therefore by using Bernoulli's equation, we have:

`(V_1^2)/(2g)+ (P_1)/(\gamma)+ z_1 + Epump= (V_2^2)/(2g)+ (P_2)/(\gamma)+ z_2+ H_L`

By dividing like terms on both sides, the equation is reduced to:

`z_1 + E_(pump) = z_2+H_L \\ \\ E_(pump) =(z_2-z_1)+H_L`

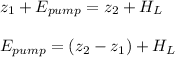
where;

`\Delta z = 400`

`\Delta z = z_2-z_1`

`\text{total head loss}= 408.5`

`E_(pump) =(400)+408.5`

`E_(pump) = 808.5 \ ft`

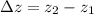
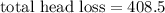
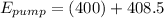
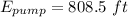
The required power input can be determined by using the formula:

`P= (\gamma_wQH_(pump))/(\eta)`

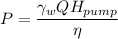
Assuming the missing pump efficiency = 70% and the flow rate Q= 1.34

Then:

`P= (62.40* 1.34 * 808.5)/(0.7)`

`P = (96576.48 \ ft.lb/s)/(550( ft*lb/s)/(hp))`

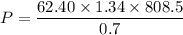
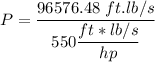
P = 175.594 hp