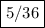Answer:
Explanation:
There are
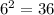 non-distinct sums that can be achieved when rolling two fair sided dice.
non-distinct sums that can be achieved when rolling two fair sided dice.
The smallest of these sums is
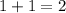 and the largest of these sums is
and the largest of these sums is
 . Within this range, there exists only one perfect cube,
. Within this range, there exists only one perfect cube,
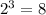 .
.
Count how many ways we can achieve a sum of 8 with two dice:
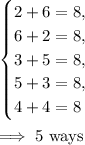
Thus the probability the total score (sum) will be a perfect cube when rolling two fair six-sided dice is equal to