Question

Write the explicit formula for the sequence below and use it to find the 16th term:

6, -24, 96, -384, . . .

Answer 1

Given:

The sequence is:

`6, -24, 96, -384,...`

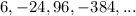
To find:

The explicit formula for the given sequence and then find the 16th term.

Solution:

We have,

`6, -24, 96, -384,...`

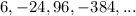
The ratio between two consecutive terms are:

`(-24)/(6)=-4`

`(96)/(-24)=-4`

`(-384)/(96)=-4`

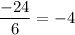
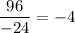
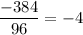
The given sequence has a common ratio. So, the given sequence is a geometric sequence with first term 6 and common ratio
`-4`.

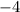The explicit formula of a geometric sequence is:

`a_n=ar^(n-1)`

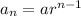
Where, a is the first term and r is the common ratio.

Putting
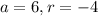`a=6, r=-4` in the above formula, we get

`a_n=6(-4)^(n-1)`

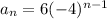
We need to find the 16th term. So, put
`n=16` in the above formula.

`a_n=6(-4)^(16-1)`

`a_n=6(-4)^(15)`

`a_n=6(-1073741824)`

`a_n=-6442450944`

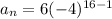
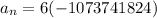
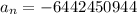
Therefore, the explicit formula for the given sequence is
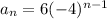`a_n=6(-4)^(n-1)` and 16th term of the given sequence is
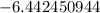`-6.442450944`.