Question

The pressure difference, , across a partial blockage in an artery (called a stenosis) is approximated by the equation where is the blood velocity, the blood viscosity , the blood density , the artery diameter, the area of the unobstructed artery, and the area of the stenosis. Determine the dimensions of the constants and . Would this equation be valid in any system of units

Answer 1

The question is incomplete. The complete question is :

The pressure difference, Δp, ac
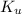`K_u`ross a partial blockage in an artery (called a stenosis) is approximated by the equation :

`$\Delta p=K_v(\mu V)/(D)+K_u\left((A_0)/(A_1)-1\right)^2 \rho V^2$`

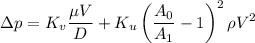
Where V is the blood velocity, μ the blood viscosity {FT/L2}, ρ the blood density {M/L3}, D the artery diameter,
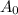`A_0` the area of the unobstructed artery, and A1 the area of the stenosis. Determine the dimensions of the constants
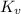`K_v` and
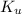`K_u`. Would this equation be valid in any system of units?

Solution :

From the dimension homogeneity, we require :

`$\Delta p=K_v(\mu V)/(D)+K_u\left((A_0)/(A_1)-1\right)^2 \rho V^2$`

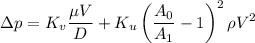
Here, x means dimension of x. i.e.

`$[ML^(-1)T^(-2)]=([K_v][ML^(-1)T^(-1)][LT^(-1)])/([L])+[K_u][1][ML^(-3)][L^2T^(-2)]$`

`$=[K_v][ML^(-1)T^(-2)]+[K_u][ML^(-1)T^(-2)]$`

So,
`$[K_u]=[K_v]=[1 ]=$` dimensionless

So,
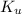`K_u` and
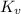`K_v` are dimensionless constants.

This equation will be working in any system of units. The constants
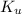`K_u` and
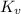`K_v` will be different for different system of units.