Given:
The figure of a right angle triangle.
A line segment intersect the two sides and parallel to third side of the triangle
To find:
The value of x.
Solution:
According to basic proportionality theorem, if a line segment intersect the two sides and parallel to third side of the triangle, then it divides the two sides proportionally.
Using basic proportionality theorem, we get
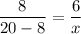
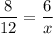
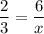
On cross multiplication, we get
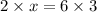
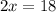
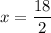
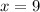
Therefore, the value of x is 9.