Question

Find the ratio of speeds of an electron and a negative hydrogen ion (one having an extra electron) accelerated through the same voltage, assuming non-relativistic final speeds. Take the mass of the hydrogen ion to be 6.7 X 10 -27 Kg.

Answer 1

v₂ /v₁ = 2.3 10⁺²

Step-by-step explanation:

The energy is conserved so the total potential energy must be transformed into kinetic energy

K = U

½ m v² = q ΔV

v =
`\sqrt{(2q \Delta V)/(m) }`

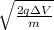
a) Let's find the speed of the electron

m = 9.1 10⁻³¹ kg

as they do not indicate the value of the power difference, we will assume that ΔV = 1 V is worth one

v =
`\sqrt{ (2 \ 1.6 \ 10^(-19) \ 1)/(9.1 \ 10^(-31)) }`

v =
`\sqrt {0.3516 \ 10^(12)}`

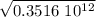
v1 = 0.593 10⁶ m / s

b) the velocity of a hydrogen ion

M = M_H + m

M = 1.673 10⁻²⁷ + 9.1 10⁻³¹

M = 1.67391 10⁻²⁷ kg

M = 1.67 10⁻²⁷ kg

v =
`\sqrt{ \frac { 2 \ 1.6 \ 10^(-19) \ 1}{1.67 \ 10^(-27)} }`

v =
`√( 1.916167 \ 10^8 )`

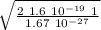
v₂ = 1.38 10⁴ m / s

the relationship between these speeds is

v₂ / v₁ = 1.38 10⁴ / 0.593 10⁶

v₂ /v₁ = 2.3 10⁺²