Question

La pirámide egipcia de keops tiene un volumen de 2;574,466 metros cúbicos su base es de 230m ¿cuál es la altura de dicha pirámide?

Answer 1

Según los datos brindados, la altura de la pirámide egipcia de Keops sería de:

• 146 metros aproximadamente.

Explanation:

Para resolver el ejercicio, debes conocer la fórmula para calcular el volumen de una pirámide cuadrangular, el cual es el tipo de pirámide al cual pertenece la pirámide de Keops:

• Volumen de una pirámide cuadrangular =
  `(L^(2) * h)/(3)`

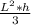
Donde:

• L = Longitud de los lados de la base cuadrada.
• h = Altura de la pirámide.

Como queremos identificar la altura, despejamos esa variable de la ecuación, pero para simplificar un poco, vamos a escribir el volumen de la pirámide con la variable "v":

• 
  `v=(L^(2) * h)/(3)`
• 
  `v * 3=L^(2) * h}`
• 
  `(v*3)/(L^(2) )=h`

Y en esta ecuación que despejamos, procedemos a reemplazar los valores de volumen y base que nos dieron en el ejercicio:

• 
  `(2574466m^(3) *3)/((230m)^(2) )=h`

Y realizamos las operaciones correspondientes:

• 
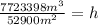  `(7723398m^(3))/(52900m^(2) )=h` (Como hay metros cúbicos en el dividendo y metros cuadrados en el divisor, simplificamos en el siguiente paso para que solo queden metros).

• 
  `h = 145.9999622m`

Aproximamos el número al entero más cercano, por lo tanto, la altura de dicha pirámide con los datos dados sería de aproximadamente 146 metros.