Answer:
The frictional force required for the car to travel is 8,365.01 N
Step-by-step explanation:
Given;
mass of the car, m = 1600 kg
radius of the curved road, r = 71 m
banking angle, θ = 15⁰
velocity of the car, v = 86 km/h = 86/3.6 = 23.89 m/s
The two forces acting on the are:
1. the parallel force to the banked plane
2. the centripetal force pushing the car up the banked plane
To keep the car traveling at 86 km/h;
frictional force + parallel force to the plane = centripetal force pushing the car up the banked plane
The parallel force to the banked plane:
F = mgsinθ
F = 1600 x 9.8 x sin(15⁰)
F = 4,057.98 N
The centripetal force pushing the car up the banked plane:
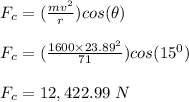
The frictional force required for the car to travel:
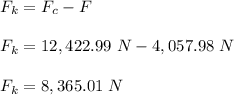
Therefore, the frictional force required for the car to travel is 8,365.01 N