Question

a 1600 kg car rounds a curve of radius 71 m banked at an angle of 15, What is the magnitude of the friction force required for the car to travel at 86 km/h

Answer 1

The frictional force required for the car to travel is 8,365.01 N

Step-by-step explanation:

Given;

mass of the car, m = 1600 kg

radius of the curved road, r = 71 m

banking angle, θ = 15⁰

velocity of the car, v = 86 km/h = 86/3.6 = 23.89 m/s

The two forces acting on the are:

1. the parallel force to the banked plane

2. the centripetal force pushing the car up the banked plane

To keep the car traveling at 86 km/h;

frictional force + parallel force to the plane = centripetal force pushing the car up the banked plane

The parallel force to the banked plane:

F = mgsinθ

F = 1600 x 9.8 x sin(15⁰)

F = 4,057.98 N

The centripetal force pushing the car up the banked plane:

`F_c= ((mv^2)/(r) )cos(\theta)\\\\F_c = ((1600 * 23.89^2)/(71) )cos(15^0)\\\\F_c = 12,422.99 \ N`

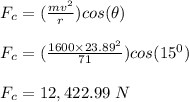
The frictional force required for the car to travel:

`F_k = F_c - F\\\\F_k = 12,422.99 \ N - 4,057.98 \ N\\\\F_k = 8,365.01 \ N`

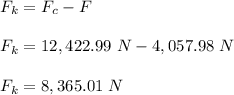
Therefore, the frictional force required for the car to travel is 8,365.01 N