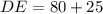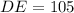Answer:

Explanation:
Given
See attachment for complete question
Required
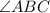 and side length DC
and side length DC
Calculating
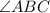
First, calculate
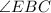
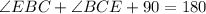 --- angles in a triang;e
--- angles in a triang;e
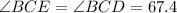
So:
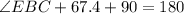
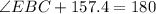
Collect like terms
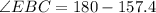
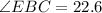
So:
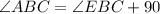
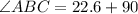

Calculating DC
First, calculate EC using Pythagoras theorem.
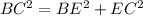
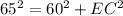
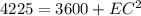
Collect like terms
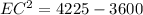

Take square roots
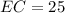
Length DC is:
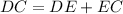
Where
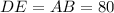
So: