Question

Question 42: Which equation represents the line that passes through the points

(-1, -2) and (3, 10)? *
O y = 3x + 1
O y = 3x - 1
O y = 4x + 2
O y = 4x - 2

Answer 1

y = 3x + 1

Explanation:

first we need to find the slope

m = (y2-y1) / (x2-x1)

m = (10 - -2) / (3 - -1) = 3

note that it does not matter which points you chose to be second or first

then use slope point equation again it does not matter which point you use

y - y1 = m ( x - x1 )

y - 10 = 3 ( x - 3)

y - 10 = 3x -9

y = 3x -9 + 10

y = 3x +1

Answer 2

Use the slope formula below (Rise Over Run)

`\large \boxed{m = (y_2 - y_1)/(x_2 - x_1) }`

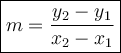
We are given two points. Substitute those points in the equation. Remember that it is (x,y) and not (y,x).

`\large{m = (10 - ( - 2))/(3 - ( -1)) } \\ \large{m = (10 + 2)/(3 + 1) \longrightarrow m = (12)/(4) } \\ \large \boxed{\purple{m = 3}}`

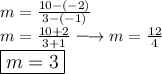
Next we will be using the point-slope form then convert into slope-intercept form. You can also use the slope-intercept form to substitute one of these points and solve for the y-intercept. However, I will be using the point-slope form instead.

`\large \boxed{y - y_1 = m(x - x_1)}`

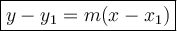
The equation above is in point-slope form. Next we can substitute one of given points. I will choose (-1,-2) to substitute (You can use another point as well since the outcome would be the same.)

`\large{y - ( - 2) = 3(x - ( - 1))}`

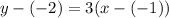
We substitute x1 = -1, m = 3 and y1 = -2. Next, we simplify the equation and convert it in slope-intercept form.

`\large{y + 2 = 3(x + 1)} \\ \large{y = 3(x + 1) - 2} \\ \large{y = 3x + 3 - 2} \\ \large \boxed{ \red{y = 3x + 1}}`

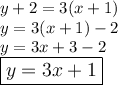
Answer

• y = 3x+1