Question

A ball is thrown horizontally from the top of a building 59 m high. The ball strikes the ground at a point 65 m horizontally away from and below the point of release. What is the speed of the ball just before it strikes the ground

Answer 1

Step-by-step explanation:

We are looking for final velocity. Since the ball is thrown horizontally, there is no upwards velocity, so the y dimension here is only useful to us for finding how long the ball was in the air. In the y dimension, here's what we know:

a = -9.8 m/s/s

Δx = -59 m

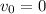`v_0=0` (again, initial upwards velocity is 0 because the ball was thrown horizontally)

We can put all that together in the equation:

Δx =
`v_0t+(1)/(2)at^2` and filling in:

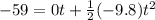`-59=0t+(1)/(2)(-9.8)t^2` which simplifies to

`-59=(1)/(2)(-9.8)t^2` and solving for t:

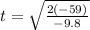`t=\sqrt{(2(-59))/(-9.8) }` and

t = 3.5 sec

Now we can use that time in the d = rt equation, which is all we need for the horizontal dimension (I'll show you why in just a second). In the horizontal dimension, here's what we know:

a = 0 m/s/s

Δx = 65 m

t = 3.5 sec

Putting that all together in our one-dimensional equation for displacement:

Δx =
`v_0t+(1)/(2)at^2` and acceleration is 0, we can simplify that down to

Δx =
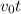`v_0t` which is the exact same thing as d = rt where r is the velocity we are looking for. Filling in:

65 = v(3.5) so

v = 18.6 m/s

That's the velocity with which the ball strikes the ground.