Answer:
5896
Explanation:
Given data set:
6283 5700 6381 6274 5700 5896 5972 6075 5993 5581 5972 6274 6075 5896
To calculate the 30th percentile;
i. Rearrange the given data set in ascending order.
5581 5700 5700 5896 5896 5972 5972 5993 6075 6075 6274 6274 6283 6381
ii. Use the following formula to get the index of the value at the 30th percentile.
N = p(n)
Where;
N = the number of data points at or below the intended percentile.
p = the intended percentile.
n = the number of points in the data.
In this case;
p = 30 percent = 0.3
n = 14
Substitute these values into the equation;
N = 0.3(14)
N = 4.2
iii. From the calculated index, find the value of the 30th percentile.
If the index is a whole number x, the desired percentile is the average of the values at index x and x+1.
For example if the index is 4, then the desired percentile is the average of the values at index 4 and 5. In our case, that will be;
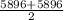 = 5896
= 5896
If the index is a decimal number, it is rounded up to the nearest integer. The value at the rounded index is the desired percentile.
For example, in our case, the index is 4.2 which when rounded up becomes 4.
Therefore, the data point or value at index 4 is the 30th percentile. From the arrangement in (ii) above, that will be 5896. i.e
5581 5700 5700 5896 5896 5972 5972 5993 6075 6075 6274 6274 6283 6381