Question

What is the equation of a circle with radius 4 and center (0,8)?

Answer 1

The equation of circle with the center at (h,k) is:

`\large \boxed{ {(x - h)}^(2) + {(y - k)}^(2) = {r}^(2) }`

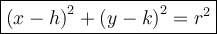
r stands for radius. Therefore r^2 = diameter or 2×radius.

The question has already given the information we need, which are:

• radius = 4
• the center at (0,8)

Since the center is (h,k) - therefore the center is at h = 0 and k = 8 making it (h,k) = (0,8).

Substitute the values in the equation:

`\large{ {(x - 0)}^(2) + {(y - 8)}^(2) = {4}^(2) }`

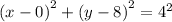
Simplify to the simplest form

`\large \boxed{ {x}^(2) + {(y - 8)}^(2) = 16} \: \: \: \: \huge{ \green{\checkmark}}`

Answer

• The equation of a circle is x^2+(y-8)^2 = 16