Question

Suppose cos(x)= -1/3, where π/2 ≤ x ≤ π. What is the value of tan(2x). EDGE

A.) -2√8/7
B.) -√8
C.) √8
D.) 2√8/7

Answer 1

D

Explanation:

We are given that:

`\displaystyle \cos x = -(1)/(3)\text{ where } \pi /2 \leq x \leq \pi`

And we want to find the value of tan(2x).

Note that since x is between π/2 and π, it is in QII.

In QII, cosine and tangent are negative and only sine is positive.

We can rewrite our expression as:

`\displaystyle \tan(2x)=(\sin(2x))/(\cos(2x))`

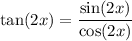
Using double angle identities:

`\displaystyle \tan(2x)=(2\sin x\cos x)/(\cos^2 x-\sin^2 x)`

Since cosine relates the ratio of the adjacent side to the hypotenuse and we are given that cos(x) = -1/3, this means that our adjacent side is one and our hypotenuse is three (we can ignore the negative). Using this information, find the opposite side:

`\displaystyle o=√(3^2-1^2)=√(8)=2√(2)`

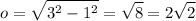
So, our adjacent side is 1, our opposite side is 2√2, and our hypotenuse is 3.

From the above information, substitute in appropriate values. And since x is in QII, cosine and tangent will be negative while sine will be positive. Hence:

`\displaystyle \tan(2x)=(2(2√(2)/3)(-1/3))/((-1/3)^2-(2√(2)/3)^2)`

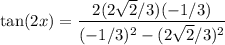
Simplify:

`\displaystyle \tan(2x)=(-4√(2)/9)/((1/9)-(8/9))`

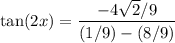
Evaluate:

`\displaystyle \tan(2x)=(-4√(2)/9)/(-7/9) = (4√(2))/(7)`

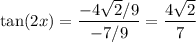
The final answer is positive, so we can eliminate A and B.

We can simplify D to:

`\displaystyle (2√(8))/(7)=(2(2√(2))/(7)=(4√(2))/(7)`

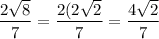
So, our answer is D.