Question

A company sells widgets. The amount of profit, y, made by the company, is related to

the selling price of each widget, x, by the given equation. Using this equation, find out
what price the widgets should be sold for, to the nearest cent, for the company to
make the maximum profit.
y = -x2 + 72x – 458

Answer 1

In order to make the maximum profit, the company should sell each widget at (the currency isn't given, so I'll be assuming USD) $36.

Explanation:

The amount of profit y made by the company from selling each widget at x price is modeled by the equation:

`y=-x^2+72x-458`

Since this is a quadratic with a negative leading coefficient, its maximum will occur at its vertex point. We want to find the price that the widget should be sold to make the maximum profit. So, we want to find the x-coordinate of the vertex. This is given by the formula:

`\displaystyle x=-(b)/(2a)`

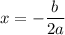
In this case, a = -1, b = 72, and c = -458. Substitute and evaluate:

`\displaystyle x=-(72)/(2(-1))=36`

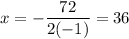
In order to make the maximum profit, the company should sell each widget at (the currency isn't given, so I'll be assuming USD) $36.