Question

Two basketballs are thrown along different paths. Determine if the basketballs’ paths are parallel to each

other, perpendicular or neither. Explain your reasoning.

o The first basketball is along the path 3x + 4y = 12
o The second basketball is along the path -6x – 8y = 24

Answer 1

Since the slopes of the two equations are equivalent, the basketballs' paths are parallel.

Explanation:

Remember that:

• Two lines are parallel if their slopes are equivalent.
• Two lines are perpendicular if their slopes are negative reciprocals of each other.
• And two lines are neither if neither of the two cases above apply.

So, let's find the slope of each equation.

The first basketball is modeled by:

`\displaystyle 3x+4y=12`

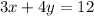
We can convert this into slope-intercept form. Subtract 3x from both sides:

`4y=-3x+12`

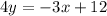
And divide both sides by four:

`\displaystyle y=-(3)/(4)x+3`

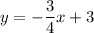
So, the slope of the first basketball is -3/4.

The second basketball is modeled by:

`-6x-8y=24`

Again, let's convert this into slope-intercept form. Add 6x to both sides:

`-8y=6x+24`

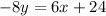
And divide both sides by negative eight:

`\displaystyle y=-(3)/(4)x-3`

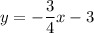
So, the slope of the second basketball is also -3/4.

Since the slopes of the two equations are equivalent, the basketballs' paths are parallel.