Question

ABCF AND EFGH ARE CONGRUENT PARALLELGRAMS. AD = 10cm, MC = 8cm, and the area of ABCD is 112cm^2. What is the number of centimeters in EN? Express your answer as a decimal to the nearest tenth

Answer 1

The image to the question is attached below.

Answer: The value of EN is 11.2 cm

Explanation:

We are given:

The parallelograms ABCD and EFGH are congruent, which simply means

AB = EF

BC = FG

CD = GH and

AD = EH

Area of ABCD = area of EFGH

Also, opposite sides of a parallelogram are equal. Thus,

AB = EF = CD = GH

BC = FG = AD = EH

It is given:

`AD=10cm=FG\\\\\text{Area of ABCD}=112cm^2=\text{Area of EFGH}`

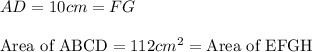
To calculate the area of a parallelogram, we use the equation:

`Area=b* h`

where, for parallelogram EFGH

b = base = FG = 10 cm

h = height = EN = ?

Area =
`112cm^2`

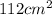
Plugging values in above equation, we get:

`112cm^2=10cm* EN\\\\EN=(112cm^2)/(10cm)=11.2cm`

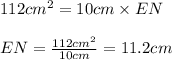
Hence, the value of EN is 11.2 cm