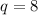Question

The demand function for a certain commodity is given by , where p is the price per unit and q is the number of units. a. At what price per unit will the quantity b. If the price is $1.87 per unit, demanded equal 8 units

Answer 1

(a) The price per unit is $1.83 when the quantity demanded is 8 units

(b) The quantity demanded is approximately 8 units when the price per unit is $1.87

Step-by-step explanation:

Given

`p = 100e^(-q/2)`

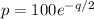
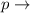`p \to` price per unit

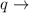`q \to` quantity demanded

Solving (a): Price per unit when quantity is 8

This means that we calculate p(8)

We have:

`p(q) = 100e^(-q/2)`

So:

`p(8) = 100e^(-8/2)`

`p(8) = 100e^(-4)`

`p(8) = 1.83`

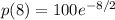
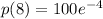
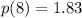
Solving (b): Quantity demanded when price per unit is $1.87

This means that:

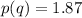`p(q) = 1.87` ---- find q

We have:

`p(q) = 100e^(-q/2)`

So:

`1.87 = 100e^(-q/2)`

Divide both sides by 100

`0.0187 = e^(-q/2)`

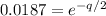
Take natural logarithm of both sides

`\ln(0.0187) = \ln(e^(-q/2))`

`-3.980 = \ln(e^(-q/2))`

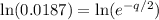
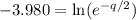
Rewrite as:

`-3.980 = -q/2}*\ln(e)`

`-3.980 = -q/2`

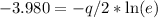
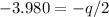
Multiply by -2

`7.96 = q`

`q = 7.96`

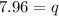
Approximate

`q = 8`