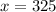Question

Melissa will rent a car for the weekend. She can choose one of two plans. The first plan has an initial fee of $65 and costs an additional $0.50 per mile driven. The second plan has no initial fee but costs per mile driven. How many miles would Melissa need to drive for the two plans to cost the same?

Answer 1

Melissa needs to drive 325 miles for the two plans to cost the same

Explanation:

Plan A

Initial Fee = 65

Additional cost per mile = 0.50 per mile

Plan B

Initial Fee = 0

Additional cost per mile = 0.70 per mile

Required

Mile both plans will cost the same

Let

`y \to cost`

`x \to miles`

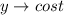
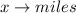
So, we have:

`y = Initial\ Fee + Additional * x`

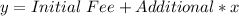
For plan A

`y = 65+ 0.50* x`

`y = 65+ 0.50x`

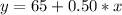
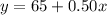
For plan B

`y = 0 + 0.70*x`

`y = 0.70x`

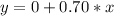
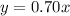
So, we have:

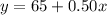`y = 65+ 0.50x` --- plan A

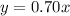`y = 0.70x` --- plan B

Both plans will cost the same when

`y = y`

`0.70x = 65 +0.50x`

`0.70x -0.50x= 65`

`0.20x= 65`

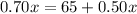
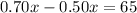
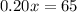
Divide by 0.20

`x= 325`