Question

In 1990, the cost of tuition at a large Midwestern university was $95 per credit hour. In 1999, tuition had risen to $221 per credit hour. Determine a linear function C(x) to represent the cost of tuition as a function of x, the number of years since 1990 C(x)= *answer here*

Answer 1

The cost of tuition as a function of x, the number of years since 1990, is C(x)= 14*(x-1990) + 95

Explanation:

A linear function is a polynomial function of the first degree that has the following form:

y= m*x + b

where

• m is the slope of the function
• n is the ordinate (at the origin) of the function

So, in this case: C(x)= m*( x-1990) + b where x is the number of years since 1990.

Given the coordinates of two points, it is possible to determine the slope m of the line from them using the following formula:

`m=(y2 - y1)/(x2 - x1)`

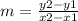
In this case, you know that in 1990, the cost of tuition at a large Midwestern university was $95 per credit hour. And in 1999, tuition had risen to $221 per credit hour. So:

• x1= 1990
• y1= 95
• x2= 1999
• y2= 221

So the value of m is:

`m=(221 - 95)/(1999 - 1990)`

`m=(126)/(9)`

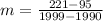
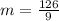
m= 14

So C(x)= 14*( x-1990) + b. In 1999, tuition had risen to $221 per credit hour. Replacing:

221= 14*(1999 - 1990) + b

221= 14*9 +b

221= 126 + b

221 - 126= b

95= b

Finally, the cost of tuition as a function of x, the number of years since 1990, is C(x)= 14*(x-1990) + 95