Question

the temperature of a cup of coffee obeys newton's law of cooling. The initial temperature of the coffee is 150F and 1 minute later it is 135F. The temperature of the room is 70F. If T(t) represents the temperature of the coffee at time T the correct differential equation for the temperature for this condition is

Answer 1

Newton's law of cooling says that:

T(t) = Tₐ + (T₀ - Tₐ)*e^(k*t)

or:

`(dT)/(dt) = -k*(T - T_a)`

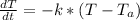
in the differential form.

where:

T is the temperature as a function of time

Tₐ is the ambient temperature, in this case, 70F

T₀ is the initial temperature of the object, in this case, 150F

k is a constant, and we want to find the value of k.

Then our equation is:

T = 70F + (150F - 70F)*e^(k*t)

Now we also know that after a minute, or 60 seconds, the temperature was 135F

then:

135F = 70F + (150F - 70F)*e^(k*60s)

We can solve this for k:

135F = 70F + 80F*e^(k*60s)

135F - 70F = 80F*e^(k*60s)

65F = 80F*e^(k*60s)

(65/80) = e^(k*60s)

Now we can apply the Ln(x) function to both sides to get:

Ln(65/80) = Ln(e^(k*60s))

Ln(65/80) = k*60s

Ln(65/80)/60s = k = -0.0035 s^-1

Then the differential equation is:

`(dT)/(dt) = -0.0035 s^-1*(T - 70F)`