Question

A complex electronic system is built with a certain number of backup components in its subsystems. One subsystem has four identical components, each with a probability of .2 of failing in less than 1000 hours. The subsystem will operate if any two of the four components are operating. Assume that the components operate independently. Find the probability that a exactly two of the four components last longer than 1000 hours. b the subsystem operates longer than 1000 hours.

Answer 1

a. 0.1536

b. 0.9728

Explanation:

The probability that a component fails, P(Y) = 0.2

The number of components in the system = 4

The number of components required for the subsystem to operate = 2

a. By binomial theorem, we have;

The probability that exactly 2 last longer than 1,000 hours, P(Y = 2) is given as follows;

P(Y = 2) =
`\dbinom{4}{2}` × 0.2² × 0.8² = 0.1536

The probability that exactly 2 last longer than 1,000 hours, P(Y = 2) = 0.1536

b. The probability that the system last longer than 1,000 hours, P(O) = The probability that no component fails + The probability that only one component fails + The probability that two component fails leaving two working

Therefore, we have;

P(O) = P(Y = 0) + P(Y = 1) + P(Y = 2)

P(Y = 0) =
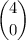`\dbinom{4}{0}` × 0.2⁰ × 0.8⁴ = 0.4096

P(Y = 1) =
`\dbinom{4}{1}` × 0.2¹ × 0.8³ = 0.4096

P(Y = 2) =
`\dbinom{4}{2}` × 0.2² × 0.8² = 0.1536

∴ P(O) = 0.4096 + 0.4096 + 0.1536 = 0.9728

The probability that the subsystem operates longer than 1,000 hours = 0.9728