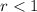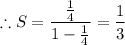Answer:
The series converges to

Explanation:
It seems to be this series:
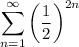
We have
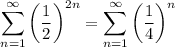
Using the Root test we can see that this series converges once
![$ \lim_(n \to \infty) \sqrt[n]a_n < 1 \implies \sum_(n=1)^(\infty) a_n \text{ is convergent}$](https://img.qammunity.org/2022/formulas/mathematics/college/hoa386q8ln2z30b7ibpw26qfxe4sso3y2d.png)
Then,
![$\lim_(n \to \infty) \sqrt[n]{\left((1)/(4) \right)^(n)} = \lim_(n \to \infty) (1)/(4) = (1)/(4) < 1$](https://img.qammunity.org/2022/formulas/mathematics/college/bve5a4qqki25zre6oifig7bdyrpwnxo5rz.png)
The series is convergent.
Once the series is geometric, the first term is
 and the ratio is also
and the ratio is also
 in this case.
in this case.
The sum of infinite geometric series is
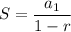 such that
such that