Answer:
1. 1080°
2. 36°
3. 27 diagonals
4. 140°
5. 7 sides
Explanation:
1. The sum S of the interior angles of a polygon is given by;
S = (n-2) x 180°
Where;
n = number of sides of the polygon.
Therefore, to get the sum of the interior angles of a polygon having 8 sides, we substitute n = 8 into equation (i) as follows;
S = (8 - 2) x 180°
S = 6 x 180°
S = 1080°
Therefore, the sum of the interior angles of a polygon having 8 sides is 1080°
2. The sum of interior angles of a polygon is given by;
S = (n - 2) x 180°
For a polygon which is a regular decagon where the number of sides n = 10, the sum is;
S = (10 - 2) x 180°
S = 8 x 180°
S = 1440°
Since the decagon is regular, then each of its interior angles is given by;
1440° / 10
=> 144°
Now, since we know that the sum of the interior angle and exterior angle will give 180°, then;
The exterior angle of a regular decagon is;
180° - 144° = 36°
Therefore, the exterior angle of a regular decagon is 36°
3. The number of diagonals N of a polygon with n sides is given by;
N =

So, for a nonagon which has 9 sides (i.e n = 9), the number of diagonals is;
N =

N =
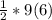
N = 9(3)
N = 27
Therefore, a nonagon has 27 diagonals.
4. The sum of interior angles of a polygon is given by;
S = (n - 2) x 180°
For a polygon which is a nonagon where the number of sides n = 9, the sum is;
S = (9 - 2) x 180°
S = 7 x 180°
S = 1260°
Since the nonagon is regular, then each of its interior angles is given by;
1260° / 9
=> 140°
Therefore, the measure of each angle (interior angle) of a regular nonagon is 140°
5. The sum of the interior angles of a polygon is given by;
S = (n - 2) x 180°
So if the sum is 900, then to get the number of sides of the polygon, we substitute S = 900 into the equation;
900° = (n - 2) x 180°
Divide through by 180°
5 = (n - 2)
Solve for n;
n = 5 + 2
n = 7
Therefore, the regular polygon has 7 sides.