Answer:
15) The length of the line segment DE is 14.908.
16) The measure of the angle W is approximately 31.792°.
17) The length of the ladder is approximately 23.182 feet.
Explanation:
15) We present the procedure to determine the length of segment DE:
(i) Determine the length of the line segment DF by trigonometric relations:
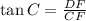 (1)
(1)
(
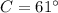 ,
,
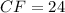 )
)
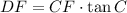
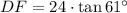
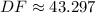
(ii) Determine the length of the line segment DE by trigonometric relations:
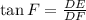 (2)
(2)
(
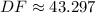 ,
,
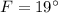 )
)
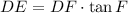
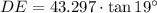
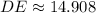
The length of the line segment DE is 14.908.
16) We present the procedure to determine the measure of the angle W:
(i) Determine the length of the line segment XZ by trigonometric relations:
 (3)
(3)
(
 ,
,
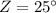 )
)
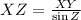
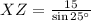

(ii) Calculate the measure of the angle W by trigonometric relations:
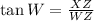 (4)
(4)
(
 ,
,
 )
)
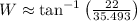
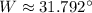
The measure of the angle W is approximately 31.792°.
17) The system form by the ladder, the ground and the wall represents a right triangle, whose hypotenuse is the ladder, which is now found by the following trigonometric relation:
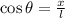 (5)
(5)
Where:
 - Angle of the ladder above ground, in sexagesimal degrees.
- Angle of the ladder above ground, in sexagesimal degrees.
 - Distance between the foot of the ladder and the base of the wall, in feet.
- Distance between the foot of the ladder and the base of the wall, in feet.
 - Length of the ladder, in feet.
- Length of the ladder, in feet.
If we know that
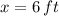 and
and
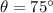 , then the length of the ladder is:
, then the length of the ladder is:
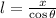
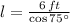
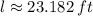
The length of the ladder is approximately 23.182 feet.