Question

Find sin 0, where is the angle shown.
Give an exact value, not a decimal approximation.

Answer 1

`\displaystyle \sin\theta=(12)/(13)`

Explanation:

Recall that in a right triangle, sine is the ratio of the opposite side to the hypotenuse:

`\displaystyle \sin\theta=\frac{\text{opposite}}{\text{hypotenuse}}`

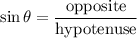
We are actually not given the opposite side in this case. However, since we know the hypotenuse and the adjacent side, we can use the Pythagorean Theorem to find the opposite side. So:

`a^2+b^2=c^2`

Let a be the adjacent side and b be the opposite side. c will be the hypotenuse.

Substitute:

`(5)^2+b^2=(13)^2`

Solve for b:

`b=√(169-25)=√(144)=12`

So, the opposite side measures 12.

Then sine will be:

`\displaystyle \sin\theta=(12)/(13)`