Question

PLEASE HELP

an artist is constructing a piece of art in the shape of rectangle. The artist wants to use string to tightly tie each vertex of rectangle to the other three vertices. The rectangle is 12.0 feet wide and 7.0 feet long. how much string should the artist use? round your answer to the nearest tenth of a foot


feet of string:

Answer 1

An artist use 51.9 feet of string for constructing a piece of art in the shape of rectangle

Explanation:

Here an artist is constructing a piece of art in the shape of rectangle having length 12 feet & width of 7 feet

Since the artist wants to use string to tightly tie each vertex of rectangle to the other three vertices. Hence one string will tie in a diagonal way

Hence total length of string will be

Total length = Perimeter of rectangle + length of diagonal

Perimeter of rectangle = 2( length + width ) = 2 ( 12 + 7 ) = 2 x 19 = 38 feet

Length of diagonal given by Pythagoras theorem

`\mathrm{Length = { \left( { a }^( 2 ) + { b }^( 2 ) \right) }^( 0.5 ) = { \left( { 12 }^( 2 ) + { 7 }^( 2 ) \right) }^( 0.5 ) = 13.89244\:\:feet}`

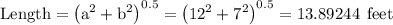
Hence

Total length = Perimeter of rectangle + length of diagonal

Total length = 38 feet + 13.89244 feet = 51.9 feet

Hence an artist use 51.9 feet of string for constructing a piece of art in the shape of rectangle