Answer:
An artist use 51.9 feet of string for constructing a piece of art in the shape of rectangle
Explanation:
Here an artist is constructing a piece of art in the shape of rectangle having length 12 feet & width of 7 feet
Since the artist wants to use string to tightly tie each vertex of rectangle to the other three vertices. Hence one string will tie in a diagonal way
Hence total length of string will be
Total length = Perimeter of rectangle + length of diagonal
Perimeter of rectangle = 2( length + width ) = 2 ( 12 + 7 ) = 2 x 19 = 38 feet
Length of diagonal given by Pythagoras theorem
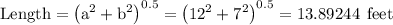
Hence
Total length = Perimeter of rectangle + length of diagonal
Total length = 38 feet + 13.89244 feet = 51.9 feet
Hence an artist use 51.9 feet of string for constructing a piece of art in the shape of rectangle