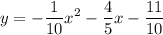Question

Write the equation for a parabola with a focus at (-4,-2) and a directrix at y = 3.

Answer 1

`\displaystyle y=-(1)/(10)x^2-(4)/(5)x-(11)/(10)`

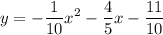
Explanation:

By definition, any point (x, y) on the parabola is equidistant from the focus and the directrix.

The distance between a point (x, y) on the parabola and the focus can be described using the distance formula:

`d=\sqrt{(x-(-4))^2+(y-(-2))^2`

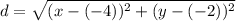
Simplify:

`d=√((x+4)^2+(y+2)^2)`

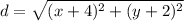
Since the directrix is an equation of y, we will use the y-coordinate. The vertical distance between a point (x, y) on the parabola and the directrix can be described using absolute value:

`d=|y-3|\text{ or } |3-y|`

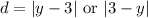
The two equations are equivalent. Therefore:

`√((x+4)^2+(y+2)^2)=|y-3|`

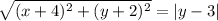
Solve for y. We can square both sides. Since anything squared is positive, we can remove the absolute value:

`(x+4)^2+(y+2)^2 = (y-3)^2`

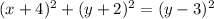
Expand:

`(x^2+8x+16)+(y^2+4y+4)=(y^2-6y+9)`

Isolate:

`x^2+8x+11=-10y`

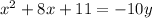
Divide both sides by -10. Hence, our equation is:

`\displaystyle y=-(1)/(10)x^2-(4)/(5)x-(11)/(10)`