Answer:
The correct option is 2.
Step-by-step explanation:
In a nuclear reaction balanced we have that:
1. The sum of the mass number (A) of the reactants (r) is equal to the sum of the mass number of the products (p)
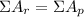
2. The sum of the atomic number (Z) of the reactants is also equal to the sum of the atomic number of the products
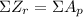
So, let's evaluate each option.
1)
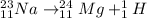
The mass number of the reactant is:
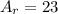
The sum of the mass number of the products is:
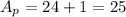
This is not the correct option because it does not meet the first condition (
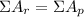 ).
).
2)
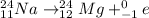
The mass number of the reactant and the products is:
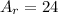
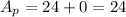
Now, the atomic number of the reactants and the products are:
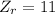
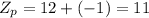
This nuclear reaction is balanced since it does meet the two conditions for a balanced nuclear equation, (
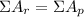 and
and
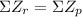 ).
).
3)
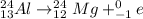
The mass number of the reactant and the products is:
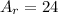
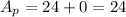
Now, the atomic number of the reactants and the products are:
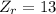
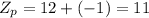
This reaction does not meet the second condition (
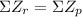 ) so this is not a balanced nuclear equation.
) so this is not a balanced nuclear equation.
4)
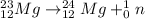
The mass number of the reactant and the products is:
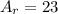
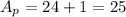
This reaction is not a balanced nuclear equation since it does not meet the first condition (
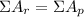 ).
).
Therefore, the correct option is 2.
I hope it helps you!