Given:
The function is:
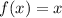
The graph of this function reflected across the x-axis. The graph is then translated 11 units up and 7 units to the left.
To find:
The equation of the transformed function.
Solution:
The translation is defined as
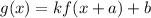 .... (i)
.... (i)
Where, k is stretch factor, a is horizontal shift and b is vertical shift.
If 0<k<1, then the graph compressed vertically by factor k and if k>1, then the graph stretch vertically by factor k.
If k<0, then the graph is reflected across the x-axis.
If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.
If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.
The graph of this function reflected across the x-axis. The graph is then translated 11 units up and 7 units to the left. So,
 . Putting these value in (i), we get
. Putting these value in (i), we get
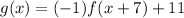
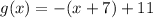
![[\because f(x)=x]](https://img.qammunity.org/2022/formulas/mathematics/high-school/1h3g0yf54oxkqbe1hq8flz8dltio9edwn8.png)
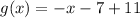
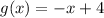
Therefore, the required function is
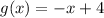 .
.