Question

Help needed to solve this ​

Answer 1

Given:

The expression is:

`(1)/(a+b)+(2a)/(a^2+b^2)+(4a^7+4a^3b^4)/(b^8-a^8)`

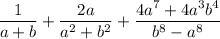
To find:

The simplified form of the given expression

Solution:

Formula used:

`x^2-y^2=(x-y)(x+y)`

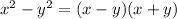
We have,

`(1)/(a+b)+(2a)/(a^2+b^2)+(4a^7+4a^3b^4)/(b^8-a^8)`

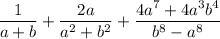
It can be written as:

`=(1)/(a+b)+(2a)/(a^2+b^2)+(4a^3(a^4+b^4))/((b^4)^2-(a^4)^2)`

`=(1)/(a+b)+(2a)/(a^2+b^2)+(4a^3(a^4+b^4))/((b^4-a^4)(b^4+a^4))`

`=(1)/(a+b)+(2a)/(a^2+b^2)+(4a^3)/((b^2-a^2)(b^2+a^2))`

`=(1)/(a+b)+(2a)/(a^2+b^2)+(4a^3)/((b-a)(b+a)(b^2+a^2))`

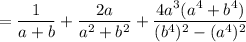
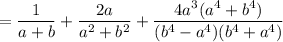
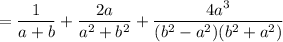
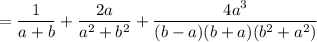
Taking LCM, we get

`=(1(b-a)(b^2+a^2)+2a(b-a)(b+a)+4a^3)/((b-a)(b+a)(b^2+a^2))`

`=(b^3+a^2b-ab^2-a^3+2a(b^2-a^2)+4a^3)/((b-a)(b+a)(b^2+a^2))`

`=(b^3+a^2b-ab^2-a^3+2ab^2-2a^3+4a^3)/((b-a)(b+a)(b^2+a^2))`

`=(b^3+a^2b+ab^2+a^3)/((b-a)(b+a)(b^2+a^2))`

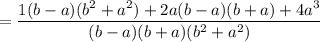
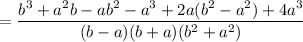
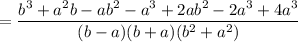
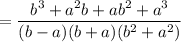
Using the grouping method factories the numerator.

`=(b(b^2+a^2)+a(b^2+a^2))/((b-a)(b+a)(b^2+a^2))`

`=((b+a)(b^2+a^2))/((b-a)(b+a)(b^2+a^2))`

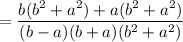
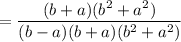
Cancel out the common factors.

`=(1)/(b-a)`

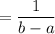
Therefore, the value of the given expression is
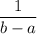`(1)/(b-a)`.