Question

Some help? Like bro literally how?!

Answer 1

Answers:

`\text{OA} = \cos(\alpha)\\\\\text{AB} = \sin(\alpha)\\\\\text{DC} = \tan(\alpha)\\\\`

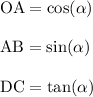
You can use the word "alpha" without quotes in place of the symbol
`\alpha` if you want (though it will depend if your teacher allows it of course).

======================================================

Step-by-step explanation:

Focus entirely on triangle AOB.

With respect to reference angle alpha (symbol
`\alpha`), the side OA is the adjacent side since it's the leg closest to or touching the reference angle.

In this same triangle, side OB is the hypotenuse. Because its the radius of the unit circle, we know that OB = 1.

We'll use the cosine rule to connect the adjacent over hypotenuse like so

`\cos(\text{angle}) = \frac{\text{adjacent}}{\text{hypotenuse}}\\\\\cos(\alpha) = \frac{\text{OA}}{\text{OB}}\\\\\cos(\alpha) = \frac{\text{OA}}{1}\\\\\text{OA} = \cos(\alpha)\\\\`

So you'll type either
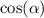`\cos(\alpha)` or cos(alpha) into the box for OA.

----------------------------------------

We're still working with triangle AOB only.

Side AB is the opposite side with respect to reference angle alpha.

We can say

sin(angle) = opposite/hypotenuse

sin(alpha) = AB/OB

sin(alpha) = AB/1

AB = sin(alpha)

Basically it's almost identical to the previous section's steps, but we're using sine instead of cosine this time. Like before, you can type in either
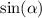`\sin(\alpha)` or sin(alpha) depending on your teacher's preferences.

----------------------------------------

This next section can be a bit tricky.

Sides AB and DC are parallel due to them being both vertical. We can use the AA (angle angle) similarity theorem to prove triangle BOA is similar to triangle DOC. The order of the letters is important. The order helps us see how the sides pair up, or how they correspond, so we can form the correct proportion.

The vertical sides of the triangles are AB and DC as mentioned earlier, so they form one fraction AB/DC. I'm dividing small over big.

Another fraction we can form is OA/OC which is dividing the horizontal legs (again small/big).

Overall, due to the similar triangles, we can set up this equation

AB/DC = OA/OC

We'll plug in what we found earlier. Also, OC = 1 because it's another radius of the same unit circle.

Lets solve for side DC.

AB/DC = OA/OC

sin(alpha)/DC= cos(alpha)/1

sin(alpha)*1 = DC*cos(alpha)

DC = sin(alpha)/cos(alpha)

DC = tan(alpha)

--------------------------------------

In summary, segments OA, AB and OC represent the cosine, sine and tangent of the reference angle alpha. These are visual ways to see how the trig ratios correspond to lengths of triangles when connecting them to the unit circle like this.

Side notes:

• Point B is at the location (cos(alpha), sin(alpha)).
• Point D is at (1, tan(alpha)).