Question

Consider the following quadratic equation. y = x2 – 8x + 4 Which of the following statements about the equation are true? The graph of the equation has a minimum. When y = 0, the solutions of the equation are a = 4 + 2V3 o When y = 0, the solutions of the equation are r x = 8 + 2V2. o The extreme value of the graph is at (4,-12). The extreme value of the graph is at (8,-4). U The graph of the equation has a maximum. Submit​

Answer 1

The graph of the equation has a minimum.

When y = 0, the solutions are
`4 \pm 2√(3)`

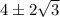
The extreme value of the graph is (4,-12).

Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

This polynomial has roots
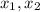`x_(1), x_(2)` such that
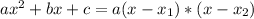`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\Delta))/(2*a)`

`x_(2) = (-b - √(\Delta))/(2*a)`

`\Delta = b^(2) - 4ac`

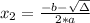
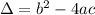
Vertex of a quadratic function:

Suppose we have a quadratic function in the following format:

`f(x) = ax^(2) + bx + c`

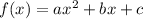
It's vertex is the point
`(x_(v), y_(v))`

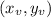
In which

`x_(v) = -(b)/(2a)`

`y_(v) = -(\Delta)/(4a)`

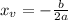
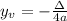
Where

`\Delta = b^2-4ac`

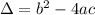
If a<0, the vertex is a maximum point, that is, the maximum value happens at
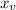`x_(v)`, and it's value is
`y_(v)`.

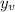y = x2 – 8x + 4

Quadratic equation with
`a = 1, b = -8, c = 4`

a is positive, so it's graph has a minimum.

Solutions when y = 0

`\Delta = b^2-4ac = 8^2 - 4(1)(4) = 64 - 16 = 48`

`x_(1) = (-(-8) + √(48))/(2) = (8 + 4√(3))/(2) = 4 + 2√(3)`

`x_(2) = (-(8) - √(48))/(2) = (8 - 4√(3))/(2) = 4 - 2√(3)`

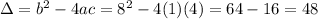
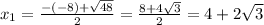
When y = 0, the solutions are
`4 \pm 2√(3)`

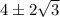
Extreme value:

The vertex. So

`x_(v) = -(-8)/(2) = 4`

`y_(v) = -(48)/(4) = -12`

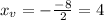
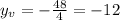
The extreme value of the graph is (4,-12).