Question

A field is a rectangle with a perimeter of 1100 feet. The length is 300 feet more than the width. Find the width and length of the rectangular field

Answer 1

Explanation:

perimeter of rectangle = 1100

let breadth be x

length = 300 + x

perimeter of rectangle = 2(l + b)

1100 = 2(300 + x + x)

1100 = 2(300 + 2x)

1100 = 600 + 4x

1100 - 600 = 4x

500 = 4x

500/4 = x

125 = x

therefore breadth is 125 feet

length = 300 + 125

=425 feet

Answer 2

The rectangular field is 425 feet by 125 feet.

Explanation:

Let w represent the width of the rectangular field.

Since the length is 300 feet more than the width, the length can be modeled by the expression (w + 300).

The perimeter of a rectangle is given by the formula:

`P=2(w+\ell)`

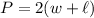
Where P is the perimeter and w and l are the width and length, respectively.

We are given that the perimeter is 1,100 feet. Substitute:

`1100=2(w+\ell)`

Divide both sides by two:

`550=w+\ell`

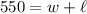
We know that l = (w + 300). So:

`550=w+(w+300)`

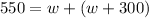
Simplify:

`2w=250`

Divide both sides by two. So, the width is:

`w=125\text{ feet}`

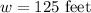
Since the length is 300 feet more than the width, that means the length is 425 feet.

The rectangular field is 425 feet by 125 feet.