Given:
Two box plots for Brand A and Brand B.
To find:
The correct statement for the given box plots.
Solution:
In a box plot, the left end of the box represents the first quartile
 , right end of the box represents the third quartile
, right end of the box represents the third quartile
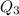 and the line inside the box represents the median.
and the line inside the box represents the median.
The interquartile range of a data set is:
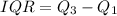
From the box plot of Brand A, it is clear that
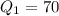
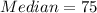
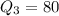
So, the interquartile range (IQR) for brand A is:

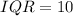
From the box plot of Brand B, it is clear that
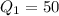
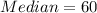
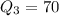
So, the interquartile range (IQR) for brand B is:
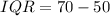
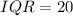
The median for brand A, $75, is greater than the median for brand B, $60.
The interquartile range (IQR) for brand A, $10, is less than the IQR
brand B. $20.
Therefore, the correct options are B and C.