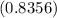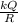Question

A charge Q is distributed uniformly around the perimeter of a ring of radius R. Determine the electric potential difference between the point at the center of the ring and a point on its axis at a distance 6R from the center. (Use any variable or symbol stated above along with the following as necessary: ke.)

ΔV = V(0) − V(6R) = ?

Answer 1

the electric potential difference between the point at the center of the ring and a point on its axis ΔV is
`( 0.8356 )`
`(kQ)/(R)`

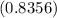
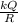
Step-by-step explanation:

Given the data in the question;

electric potential at the center of the ring V₀ = kQ / R

electric potential on the axis point Vr = kQ / √( R² + x² )

at a distance 6R from the center,

point at x = 6R

so distance circumference r = √( R² + (6R)² )

so

electric potential on the axis point Vr = kQ / √( R² + (6R)² )

Vr = kQ / R√37

Now

ΔV = V₀ - Vr

we substitute

ΔV = ( kQ / R) - ( kQ / R√37 )

ΔV = kQ/R( 1 - 1/√37 )

ΔV = kQ/R( 1 - 0.164398987 )

ΔV = kQ/R( 0.8356 )

ΔV =
`( 0.8356 )`
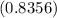
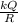`(kQ)/(R)` { where k =
`(1)/(4\pi e_0)` }

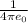Therefore, the electric potential difference between the point at the center of the ring and a point on its axis ΔV is
`( 0.8356 )`
`(kQ)/(R)`