Question

Vectors 퐴, 퐵and 퐶are added together. 퐴has a magnitude of 20.0 units and makes an angle of 60.0° counterclockwise from the negativex-axis. 퐵has a magnitude of 40.0 units and makes an angle of 30.0° counterclockwise from the positive x-axis.퐶has a magnitude of 35.0 units and makes an angle of 60.0° clockwise from the negative y-axis. Determine the magnitude of the resultant vector 퐴+퐵+퐶and its direction as an angle measured counterclockwise from the positive x-axis.

Answer 1

Magnitude = 15.86 units

direction = 69 degree below negative X axis

Step-by-step explanation:

A = 20 units at 60.0° counterclockwise from the negative x - axis

B = 40 units at 30.0° counterclockwise from the positive x - axis

C = 35 units at 60.0° clockwise from the negative y - axis

Write the vectors in the vector form

`\overrightarrow{A} =20 (- cos 60 \widehat{i} - sin 60 \widehat{j})=- 10\widehat{i} - 17.3 \widehat{j}\\\\\overrightarrow{B} =40 (cos 30 \widehat{i} + sin 30 \widehat{j})= 34.6\widehat{i} +20 \widehat{j}\\\\\overrightarrow{C} =35 (- sin 60 \widehat{i} - cos 60 \widehat{j})=- 30.3\widehat{i} - 17.5 \widehat{j}\\\\Now\\\\overrightarrow{A} + \overrightarrow{B} + \overrightarrow{C} = (- 10 + 34.6 - 30.3) \widehat{i} + (-17.3 + 20-17.5)\widehat{j}\\\\`

`\\\overrightarrow{A} + \overrightarrow{B} + \overrightarrow{C} = - 5.7\widehat{i} -14.8\widehat{j}`

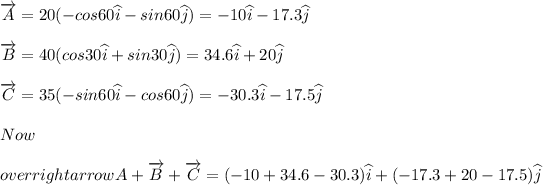
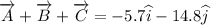
The magnitude is given by

`= √(5.7^2 + 14.8^2) = 15.86 units`

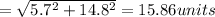
The direction is given by

`tan\theta = (- 14.8)/(- 5.7)\\\\\theta= 69^o`

below negative X axis.