Answer: The amount of heat needed to melt the given amount of octane is 84.6 kJ
Step-by-step explanation:
We know:
Boiling point of Octane =
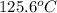
Few processes involved are:
(1):
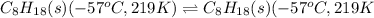
(2):
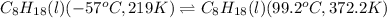
Calculating the heat absorbed for the process having same temperature:
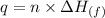 ......(i)
......(i)
where,
q is the amount of heat absorbed, n is the moles of sample and
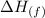 is the enthalpy of fusion
is the enthalpy of fusion
Calculating the heat released for the process having different temperature:
 ......(ii)
......(ii)
where,
n = moles of sample
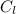 = specific heat of liquid
= specific heat of liquid
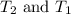 are final and initial temperatures respectively
are final and initial temperatures respectively
The number of moles is defined as the ratio of the mass of a substance to its molar mass.
The equation used is:
 ......(3)
......(3)
Given mass of octane = 160. g
Molar mass of octane = 114.23 g/mol
Plugging values in equation 3:
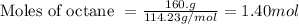
We are given:
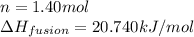
Putting values in equation (i), we get:
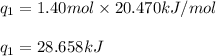
We are given:
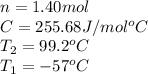
Putting values in equation (ii), we get:
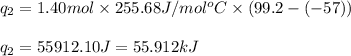
Calculating the total amount of heat released:
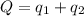
![Q=[(28.658)+(55.912)]kJ=84.6kJ](https://img.qammunity.org/2022/formulas/chemistry/college/bohe432tpgp0ogf7h7dg2rewmpcy3h7woz.png)
Hence, the amount of heat needed to melt the given amount of octane is 84.6 kJ