Question

The radius of a right circular cone is increasing at a rate of 1.1 in/s while its height is decreasing at a rate of 2.6 in/s. At what rate is the volume of the cone changing when the radius is 107 in. and the height is 151 in.

Answer 1

The volume of the cone is increasing at a rate of 1926 cubic inches per second.

Explanation:

Volume of a right circular cone:

The volume of a right circular cone, with radius r and height h, is given by the following formula:

`V = (1)/(3) \pi r^2h`

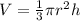
Implicit derivation:

To solve this question, we have to apply implicit derivation, derivating the variables V, r and h with regard to t. So

`(dV)/(dt) = (1)/(3)\left(2rh(dr)/(dt) + r^2(dh)/(dt)\right)`

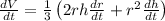
Radius is 107 in. and the height is 151 in.

This means that
`r = 107, h = 151`

The radius of a right circular cone is increasing at a rate of 1.1 in/s while its height is decreasing at a rate of 2.6 in/s.

This means that
`(dr)/(dt) = 1.1, (dh)/(dt) = -2.6`

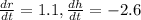
At what rate is the volume of the cone changing when the radius is 107 in. and the height is 151 in.

This is
`(dV)/(dt)`. So

`(dV)/(dt) = (1)/(3)\left(2rh(dr)/(dt) + r^2(dh)/(dt)\right)`

`(dV)/(dt) = (1)/(3)(2(107)(151)(1.1) + (107)^2(-2.6))`

`(dV)/(dt) = (2(107)(151)(1.1) - (107)^2(2.6))/(3)`

`(dV)/(dt) = 1926`

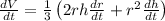
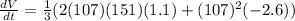
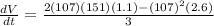
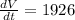
Positive, so increasing.

The volume of the cone is increasing at a rate of 1926 cubic inches per second.