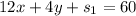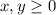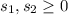Question

. A company produces two products, A and B, which have profits of $9 and $7, respectively. Each unit of product must be processed on two assembly lines, where the required production times are as follows. Product Hours/Unit Line 1 Line 2 A 12 4 B 4 8 Total hours 60 40 a) Formulate a linear programming model to determine the optimal product mix that will maximize profit. b) Transform this model into standard form.

Answer 1

(a) Linear model

`max\ P = 9x + 7y`

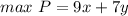
Subject to:

`12x + 4y \le 60`

`4x + 8y \le 40`

`x,y \ge 0`

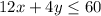
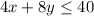
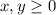
(b) Standard form:

`max\ P = 9x + 7y`

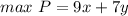
Subject to:

`12x + 4y + s_1 = 60`

`4x + 8y +s_2= 40`

`x,y \ge 0`

`s_1,s_2 \ge 0`

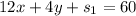
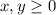
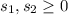
Step-by-step explanation:

Given

`\begin{array}{ccc}{} & {Hours/} & {Unit} & {Product} & {Line\ 1} & {Line\ 2} & {A} & {12} & {4} & {B} & {4} & {8} & {Total\ Hours} & {60} &{40}\ \end{array}`

Solving (a): Formulate a linear programming model

From the question, we understand that:

A has a profit of $9 while B has $7

So, the linear model is:

`max\ P = 9x + 7y`

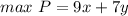
Subject to:

`12x + 4y \le 60`

`4x + 8y \le 40`

`x,y \ge 0`

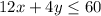
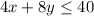
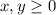
Where:

`x \to line\ 1`

`y \to line\ 2`

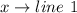
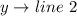
Solving (b): The model in standard form:

To do this, we introduce surplus and slack variable "s"

For
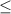`\le` inequalities, we add surplus (add s)

Otherwise, we remove slack (minus s)

So, the standard form is:

So, the linear model is:

`max\ P = 9x + 7y`

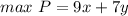
Subject to:

`12x + 4y + s_1 = 60`

`4x + 8y +s_2= 40`

`x,y \ge 0`

`s_1,s_2 \ge 0`