Question

A particle with charge q1 = +4.0 µC is located at x = 0, and a second particle with charge q2 = −2.1 µC is located at x = 15 cm. Determine the location of a third particle with charge q3 = +4.6 µC such that the net electric field at x = 25 cm is zero.

Answer 1

x₃ = 0.0725 m

Step-by-step explanation:

The force between the particles is electrical

F =
`k (q_1q_2)/(r_(12)^2)`

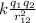
F = q₀ E_total

don q₀ is a positive test charge at the point of interest, therefore we can calculate the electric field at the point of interest x₀ = 0.25 cm

F = 0 → E_total = 0

E_total = E₁ + E₂ + E₃

E_total =
`k (q_1)/(r_(1o)^2) + k (q_2)/(r_(2o)^2) + k (q_3)/(r_(3o)^2)`

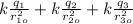
E_total = k (
`(q_1)/(r_(1o)^2) + (q_2)/(r_(2o)^2) + (q_3)/(r_(3o)^2)` )

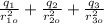let's look for the distances

r₁₀ = (x₀ - 0)

r₁₀ = 0.25 m

r₂₀ = √(x₀ - x₂) ²

r₂₀ = √ (0.25 - 0.15) ²

r₂₀ = 0.10 m

r₃₀ = √ (0.25 - x₃) ²

we substitute

0 = 9 10⁹ (4 / 0.25² - 2.1 / 0.1² + 4.6 / (0.25-x₃)² )

4.6 / (0.25-x3)² = -4 / 0.25² + 2.1 / 0.1²

4.6 / (0.25-x3) ² = -146

(0.25 - x3) ² = - 4.6 / 146 = - 0.0315068

0.25 - x3 = 0.1775

x₃ = 0.25 - 0.1775

x₃ = 0.0725 m