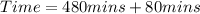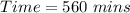Question

An ancient Chinese candle clock tells the amount of time that has passed by the amount of wax that has been melted off the candle. Each candle is divided into 121212 sections, marked 111 inch (\text{in})(in)(, start text, i, n, end text, )apart. It takes 444 hours (\text{hrs})(hrs)(, start text, h, r, s, end text, )for each candle to completely melt, after which a new candle is lit. If two candles have completely melted and one candle has melted 4\ \text{in}4 in4, space, start text, i, n, end text, how many minutes have passed since the first candle was lit

Answer 1

`Time = 560\ mins`

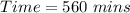
Explanation:

Given

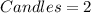`Candles = 2` --- candles melted

`Divisions = 12`

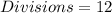
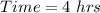`Time = 4\ hrs` --- time to melt

Required

The time since the first was lit

If 1 candle melts in 4 hours, 2 candles will melt in 8 hours.

i.e.

`x = Candles * Time`

`x = 2 * 4hrs`

`x = 8hrs`

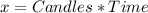
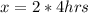
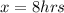
For the 3rd candle that has melted, 4 inches

First, calculate the fraction that melt

`Fraction = (Melt)/(Division)`

`Fraction = (4)/(12)`

`Fraction = (1)/(3)`

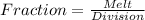
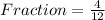
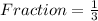
The time to melt is:

`y = Fraction * Time`

`y= 4 * (1)/(3)`

`y= (4)/(3)hrs`

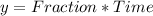
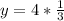
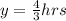
So, the required time is:

`Time = x + y`

`Time = 8hrs + (4)/(3)hrs`

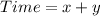
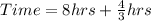
Convert to minutes

`Time = 8*60mins + (4)/(3)*60mins`

`Time = 480mins + 80mins`

`Time = 560\ mins`