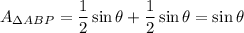Question

Can someone please help me with this?? I will like your comment!

Answer 1

`A_(\Delta ABP)=\sin \theta`

Explanation:

Let the center of the circle be O.

Recall that the area of a triangle can be given by:

`\displaystyle A=(1)/(2) ab\sin C`

Where C is the angle between the two sides.

ΔABP is equal to the sum of ΔAPO and ΔBOP.

Let a = OP and b = OB. Since this is the unit circle and PO and BO are radii, they both equal one. C will be θ. Hence, the area of ΔBOP is:

`\displaystyle A_(\Delta BOP)=(1)/(2)(1)(1)\sin \theta=(1)/(2)\sin\theta`

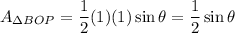
For ΔAPO, we can use the two sides OP and OA. Again, they are the radii of the unit circle, so they equal one. The angle in this case will be π - θ radians. Hence:

`\displaystyle A_(\Delta APO)=(1)/(2)(1)(1)\sin\left(\pi -\theta\right)=(1)/(2)\sin\left(\pi -\theta\right)`

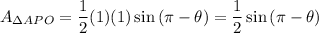
However, note that sin(π - θ) = sin(θ). Hence:

`\displaystyle A_(\Delta APO)=(1)/(2)\sin\left(\theta\right)`

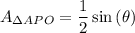
Hence, the area of ΔABP is:

`\displaystyle A_(\Delta ABP)=(1)/(2)\sin \theta+(1)/(2)\sin\theta =\sin \theta`