Question

Cosy/1-siny = 1+siny/cosy
varify using trig identity.

Answer 1

See Below.

Explanation:

We want to verify the equation:

`\displaystyle (\cos y)/(1-\sin y)=(1+\sin y)/(\cos y)`

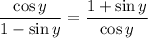
On the left, we can multiply both layers by (1 + sin(y)):

`\displaystyle (\cos y)/(1-\sin y)\left((1+\sin y)/(1+\sin y)\right)=(1+\sin y)/(\cos y)`

Multiply:

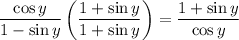
`\displaystyle (\cos y(1+\sin y))/(1-\sin^2 y)=(1+\sin y)/(\cos y)`

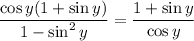
From the Pythagorean Theorem, we know that sin²(y) + cos²(y) = 1. Hence, 1 - sin²(y) = cos²(y). Substitute:

`\displaystyle (\cos y(1+\sin y)))/(\cos^2 y)=(1+\sin y)/(\cos y)`

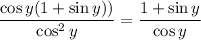
Cancel:

`\displaystyle (1+\sin y)/(\cos y)=(1+\sin y)/(\cos y)`

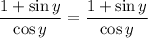
Hence proven.