Question

Perform the following

mathematical operation, and
report the answer to the
correct number of significant figures.

7.68 x 4.564 = [?]

Answer 1

Answer: The correct number of significant figures in
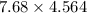`7.68 * 4.564` is 35.05152.

Step-by-step explanation:

Digits present in a number that helps in determining the degree of accuracy starting from the first non-zero digit is called a significant figure.

Some rules for significant figures are as follows.

• All the digits present within the non-zero digits are considered in a number.

For example, 2085 contains 4 significant digits.

• Leading zeros are not counted in a number.

For example, 0.0034 has 2 significant digits.

• We count the trailing zeros when a decimal point is present in a number.

For example, 0.02500 has 4 significant figures.

• When there is no decimal point then trailing zeros may or may not count.

For example, 19000 has 2 significant digits.

Now, the product of given digits is as follows.

`7.68 * 4.564 = 35.05152`

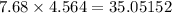
Thus, we can conclude that correct number of significant figures in
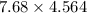`7.68 * 4.564` is 35.05152.