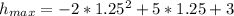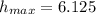Question

Michelle throws a frisbee into the air. The height of the frisbee at a given time can be modeled by the equation h(t)= -2t

Answer 1

(a) The ball will hit the ground after 3 seconds

(b) The maximum height is 6.125

Explanation:

Given

`h(t) = -2t^2 +5t +3`

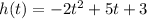
Solving (a): When the frisbee will hit the ground?

To do this, we set h(t) to 0

So, we have:

`h(t) = -2t^2 +5t +3`

`-2t^2 +5t +3=0`

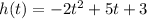
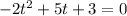
Expand

`-2t^2 +6t-t +3=0`

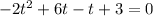
Factorize

`-2t(t - 3) -1(t - 3) = 0`

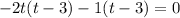
Factor out t - 3

`(-2t -1)(t - 3) = 0`

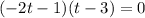
Split:

`-2t -1= 0\ or\ t - 3 = 0`

Solve for t in both equations

`-2t =1\ or\ t = 3`

`t =-(1)/(2)\ or\ t = 3`

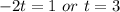
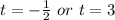
Time can't be negative; So:

`t = 3`

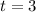
Solving (b): How height the frisbee will go?

First, we calculate time to reach the maximum height

`t = -(b)/(2a)`

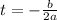
Where:

`h(t) = at^2 + bt + c`

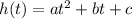
By comparison:

`a = -2,\ b =5,\ c =3`

So:

`t = -(b)/(2a)`

`t = -(5)/(2*-2)`

`t = (5)/(4)`

`t = 1.25`

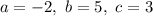
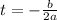
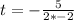
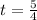
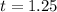
So, the maximum height is:

`h_(max) = -2 * 1.25^2 + 5 * 1.25 + 3`

`h_(max) = 6.125`