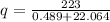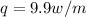Answer:
Step-by-step explanation:
From the question we are told that:
Ground-to-cable-center line Distance
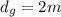
Diameter of Cable case
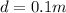
Temperature of Nitrogen
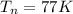
Insulator
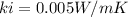
Thickness
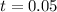
Mass
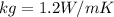
Temperature of earth surface
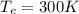
Generally the equation for Heat rate per unit length is mathematically given by
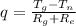
Where
![R_g=[kg((2\pi)/((in4d_g/d_x))]^(_1)](https://img.qammunity.org/2022/formulas/engineering/college/bse17m9fuu7peuzidcodbt2jybdn2l8z8n.png)
![R_g=[(1.2)((2\pi)/((in4(2)/0.2))]^(-1)](https://img.qammunity.org/2022/formulas/engineering/college/dxqgafaqv49e08tjwdz1itwt2zot13fseb.png)
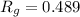
And
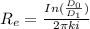

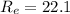
Therefore