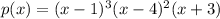Question

Write the general polynomial p(x) if its only zeros are 1 4 and -3 with multiplicites 3 2 and 1 respectively what is the degree

Answer 1

The 6th degree polynomial is
`p(x) = (x-1)^3(x-4)^2(x+3)`

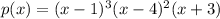
Explanation:

Zeros of a function:

Given a polynomial f(x), this polynomial has roots
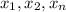`x_(1), x_(2), x_(n)` such that it can be written as:
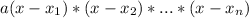`a(x - x_(1))*(x - x_(2))*...*(x-x_n)`, in which a is the leading coefficient.

Zero 1 with multiplicity 3.

So

`p(x) = (x-1)^3`

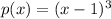
Zero 4 with multiplicity 2.

Considering also the zero 1 with multiplicity 3.

`p(x) = (x-1)^3(x-4)^2`

Zero -3 with multiplicity 1:

Considering the previous zeros:

`p(x) = (x-1)^3(x-4)^2(x-(-3)) = (x-1)^3(x-4)^2(x+3)`

Degree is the multiplication of the multiplicities of the zeros. So

3*2*1 = 6

The 6th degree polynomial is
`p(x) = (x-1)^3(x-4)^2(x+3)`